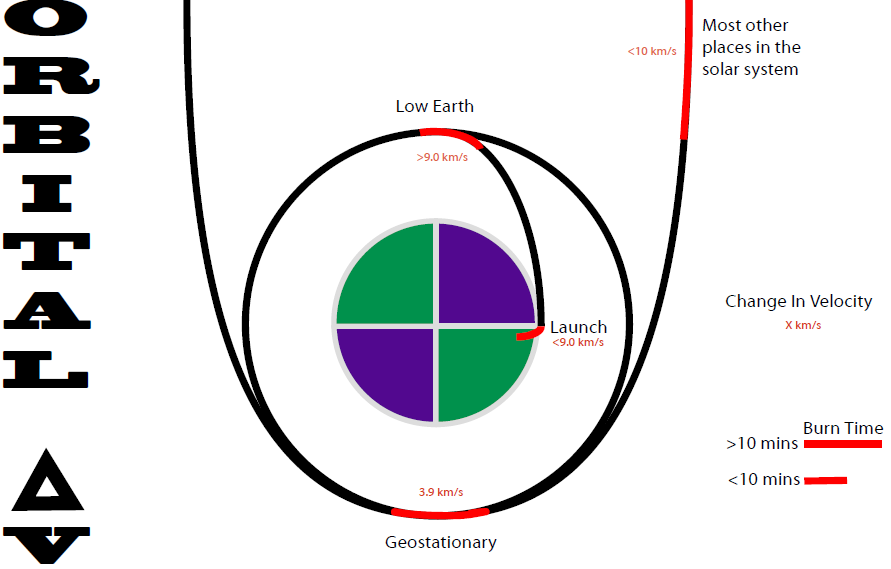
Na początek, mogłeś słyszeć o “zasięgu” statku kosmicznego w science fiction. Jednakże, pojazdy kosmiczne tak nie działają; jesteś na orbicie, jeśli wyłączysz silniki, nie przestaniesz się ruszać, będziesz wciąż podążał po orbicie, bo w kosmosie nie ma tarcia, które mogłoby cię spowolnić. Żeby naprawdę wiedzieć, do czego zdolna jest rakieta, musisz wiedzieć ile delta-v posiada.
Delta V (`∆V`, dosłownie "zmiana prędkości") jest ważne, bo określa, jak bardzo możesz zmienić swoją orbitę. Jeśli jesteś na okrągłej orbicie, przyspieszenie podniesie przeciwną stronę orbity, a zwolnienie ją obniży. Jeśli chcesz lecieć z, powiedzmy, niskiej orbity okołoziemskiej (Low Earth Orbit - LEO) na geostacjonarną orbitę transferową (Geostationary Transfer Orbit - GTO), musisz przyspieszyć o konkretną prędkość. W tym przypadku z GTO, potrzebna zmiana prędkości wynosi około `2,5 (km)/s`, co oznacza, że twoja rakieta potrzebuje `2,5 (km)/s` delta-v, aby osiągnąć tę orbitę. Aby obliczyć delta-v rakiety albo pojazdu kosmicznego musimy użyć wzoru Ciołkowskiego:
`∆V=Ve*ln(m_0/m_1)`
Gdzie `Ve` jest prędkością wylotową (prędkość, z jaką gazy opuszczają silnik), `m_0` jest masą początkową, a `m_1` jest masą końcową. ln jest logarytmem naturalnym. `m_0/m_1` jest też nazywane liczbą Ciołkowskiego (R), która jest stosunkiem mas, co jest użyteczne przy liczeniu masy, kiedy znasz delta-v.
Jeśli spojrzysz na parametry rakiet, często zobaczysz termin "impuls właściwy" albo `Isp`. Prawdopodobnie nic to dla ciebie nie znaczy. Właściwie jest to prędkość wylotowa (`Ve`) podzielona przez przyspieszenie grawitacyjne, oznaczane `g`. Zostało wymyślone, kiedy niemieccy i amerykańscy naukowcy mieli problemy związane z używaniem różnych jednostek prędkości wylotowej, a musieli pracować razem, więc podzielili prędkość wylotową przez przyspieszenie grawitacyjne (9,81 w systemie metrycznym, 32,3 w jednostkach imperialnych) i otrzymali tę samą liczbę, co ułatwiło dzielenie się informacjami. A więc, `V_e` to `Isp*9,81` jeśli używasz jednostek metrycznych (a powinieneś).
Zaprezentujmy przykład działania tego wzoru. Weźmy rakietę, której masa wraz z paliwem wynosi 10 000 kilogramów, a masa pustej rakiety wynosi 2000 kilogramów i ma silnik, którego impuls właściwy wynosi 450:
`∆V=450*9,81*ln(10000/2000)=7104,86 m/s`
Zauważ, że to nie konkretne liczby ważą na wyniku, a stosunek pomiędzy nimi. Na przykład, jeśli użyjesz funtów jako jednostek, to zmieniłoby się na `22000/4400` albo ton `10/2`, a stosunek pozostanie taki sam, to otrzymasz ten sam wynik. Dodatkowo, jeśli zdecydujesz się użyć amerykańskich jednostek (nie wiem, czemu miałbyś chcieć to zrobić), to możesz wstawić prędkość wylotową w `(ft)/s` (stopa na sekundę) i wciąż otrzymasz `∆V` w `(ft)/s`.
Pamiętaj, że jeśli masz parametry rakiety, to do mas musisz dodać masę ładunku. Weźmy na przykład górny stopień Centaur używany na Altasie V, który waży około 22 tony z paliwem i 2 tony pusty i dajmy mu ładunek 5 ton:
`∆V= 450*9,81*ln(27/7)=5959,25 m/s`
Teraz możesz chcieć osiągnąć konkretne delta-v, powiedzmy `3140 m/s`, żeby osiągnąć księżycową trajektorię transferową (Trans Lunar Injection - TLI) (to orbita, której jedna strona umieszcza cię tak blisko Księżyca, że możesz go zacząć orbitować) i powiedzmy, że masz Centaura na LEO, w pełni zatankowanego i gotowego do lotu. Jak duży ładunek mógłbyś umieścić na TLI?
Aby to obliczyć, możesz wziąć równanie i podstawić liczby w ten sposób:
`3140=450*9.81*ln((22+x)/(2+x))`
22 i 2 to odpowiednio masa pełnego i pustego Centaura, a `x` to masa ładunku. Teraz mógłbyś obliczyć to własnoręcznie przy użyciu wymyślnej matematyki, ale jeśli nie wiesz jak to zrobić, albo nie masz na to czasu/ochoty, możesz wstawić te liczby w kalkulator graficzny lub użyć np. strony Wolfram Alpha, aby otrzymać masę ładunku. Pod "solution", naciśnij "approximate form", aby otrzymać liczbę. W naszym przypadku jest to 17,293 ton. Możesz podstawić liczby w drugą stronę, jeśli jesteś paranoikiem.
Jeśli masz konkretny ładunek i konkretne delta V, ale nie wiesz, jak duży musi być stopień wynoszący, możesz go obliczyć na podstawie PMF. PMF to Propellant Mass Fraction (ułamek masy paliwa) stopnia rakiety; to masa paliwa w rakiecie podzielona przez masę rakiety. Im wyższy PMF, tym bardziej wydajny masowo jest stopień. Dla naszego Centaura jest to `20/22=0,9`. Aby otrzymać masę stopnia, możesz rozwiązać to równanie:
`∆V=Isp*g*ln((P+x)/(P+(1-PMF)*x))`
Gdzie P to masa ładunku, a PMF to PMF. Powiedzmy, że chcemy wysłać 10-tonowy ładunek na TLI stopniem o PMF wynoszącym 0,9 i Isp wynoszącym 450:
`3140=450*9.81*ln((10+x)/(10+0.1x))`
`x = 13,017 t`
Gratulacje! Właśnie ukończyłeś swoją pierwszą lekcję dotyczącą rakiet. Teraz pewnie chciałbyś wiedzieć, ile delta-v potrzeba, aby lecieć w różne miejsca, takie jak Księżyc czy Mars. Na Wikipedii jest o tym artykuł z tabelkami i rysunkami.